Os triângulos são polígonos que, dependendo do valor de seus lados e ângulos, podem possuir características diferentes, por exemplo: quando um triângulo tiver um ângulo reto (igual a 90°) ele será chamado de triângulo retângulo. Nesse tipo de triângulo podemos fazer uma relação entre seus lados que foi desenvolvida por Pitágoras, assim nomeada como Teorema de Pitágoras.
Foi através dos números pitagóricos (três números inteiros que servem de medida para os lados de um triângulo retângulo) que chegamos à relação dos lados de um triângulo retângulo. Veja como foi provada essa relação:
Considere um quadrado de vértices ABCD, iremos dividir cada lado em duas partes que medirão a e b:
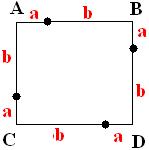
Os pontos que separam as medidas a e b serão P, Q, R, S:
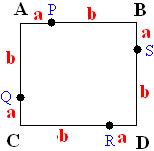
A união desses pontos irá formar um quadrado de lado de medida c.
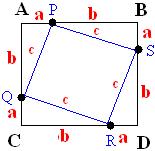
A área do quadrado ABCD é igual a (a+b) . (a+b) ou igual à área do quadrado PQRS mais a área dos triângulos PAQ, QCR, RDS e PBS. Veja a representação algébrica desses cálculos:
AABCD = (a+b) . (a+b)
AABCD = (a+b)2
OU
Como todos os triângulos são iguais podemos representar a soma de todos por: 4 . A∆SRD. Assim, a outra forma de calcularmos a área do quadrado ABCD é:
AABCD = A PQRS + 4 . A∆SDR
Como os lados do quadrado PQRS são iguais a c, sua área será c2. E como a base do triângulo SRD é igual a a e a altura igual a b, podemos dizer que a área do triângulo SRD é igual a ab / 2. Substituindo essas deduções, teremos:
AABCD = c2 +4 . ab / 2
(a+b)2 = c2 +4 . ab / 2
a2 + 2ab + b2 = c2 +4 . ab / 2
2a2 + 4ab + 2b2 = 2c2 + 4ab
2 2
2a2 + 2b2 = 2c2
a 2 + b2 = c2
O triângulo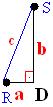 é retângulo no vértice D, portanto a relação feita entre seus lados é:
é retângulo no vértice D, portanto a relação feita entre seus lados é:
a2 + b2 = c2
Não pare agora... Tem mais depois da publicidade ;)
Por Danielle de Miranda
Graduada em Matemática
Equipe Brasil Escola